史蒂文˙林斯Steven Rings,芝加哥大学教授,研究侧重于转换理论、现象学、流行音乐和声音。著作《调性与转换》(Tonality and Transformation)。
6月28日,林斯教授继续将音调和“转换理论”以及“广义音程”进行了延展式的讲解,继而进入到转换理论的子领域——“新黎曼理论”的导入与延伸。
为了正确完整陈述林斯教授的课程内容与观点,这里笔者以最简短的话语将前一天林斯教授对“广义音程”(GIS,或者也可称为广义距离体系)与“转换理论”(Transformational)作一点回顾。转换模式代表了从客观外部的观察者,以“广义音程”为视角,积极参与至音乐的过程中,这似乎是一种微妙的,有点难以捉摸的概念,表现为将找到的某种关联以一种带有方向感的因素以箭头标记式贯穿于音乐当中的体验。可以想象面对一个整体,分析后可以出现很多不同的体验,转化理论更强调复合式的结果,没有唯一的“interval”,这样就会导致与以往不同的分析路径。这正是这个理论有魅力的部分,但也会在初期出现困惑。在申克分析理论中,你会有清晰的研究方向,但在转换理论中,你在初期似乎没有准确的起始点,你需要选择起始点,寻找更为丰富的角度。
昨天,教授更多的强调概念化的“interval”,今天,具体的进入到“转换”,课程中再一次展示了这个“转换理论”观点的基本图示。
从s到t,i以箭头的方向性代表了“interval”,“箭头”被认为是一种音乐行为,这就是“转换”的态度,这里强调的是非被动化的理解。想象身处s点,为了到达t点,我们可以从不同的角度理解这个过程。如,摆在我们面前的两个音,不应该只是习惯性的把单独的音符当作音程来看,更应该是一种音乐形态。以s-t为例,“转换”的态度不是以关注其中的连接为唯一目的,而是s应该是以什么有特性的方式(i)到达t点。
如果由基本图示引申出两个空白的圈,我们可以将音乐B和C填充到这两个圈中,我们应该关注的是B将以什么样的音乐行为到达C,而B和C代表着什么?不是确定的,可能是音高、音高集合、半音阶、全音阶等等,这些都是可能会影响到我们所说的“转换”。
继而,教授以这样简单的“音”到“音”的不同进行来解释他的观点。“Step”这里指音级式进阶,与之对应的是另一种进行,“ResC”——解决。

(a)是如同有“地心引力”的,(b)则是中立性的。(a)与(b)中虽然都有B?C,但却并不是一样的音乐行为。区别就是,(a)有强烈的方向性,而(b)则是一对一的,这样就会有(c)的反向操作,我们发现,Step是可逆的,如果这样理解“Step”,那么就与列文(Levin)的“转换”思想有微妙的关联,那就是:有更多的“转换”不能被当作音程,“转换”的范围要广于音程的转换,这也是为什么“转换理论”不是音程理论,“转换”映射了更加广阔的范围。
林斯教授分别以两个范例做了详尽的剖析。
Schubert,Piano Sonata,D.664,mvt.2(analysis:Rings)
舒伯特著名的D.664钢琴奏鸣曲,第二乐章开端。(b)是林斯教授剥离出的音高行进。从图中已经可以清晰的看到动机发展的方式,按照以往分析观点来看,图(b)已经极为清晰的展示出了这里音乐的内在关系。林斯教授其后的分析图例可以看出更多维度的理解,在几张图例的并列展示中,也可以看到这里的“音乐行为”是以不同的转换动作得以完成。
+/-(n)代表自然音级的变化,箭头代表了方向,从中清楚的看到X-X’、以及其后变型单位Y、低音,等等不同单位在空间与方向上的轮廓。
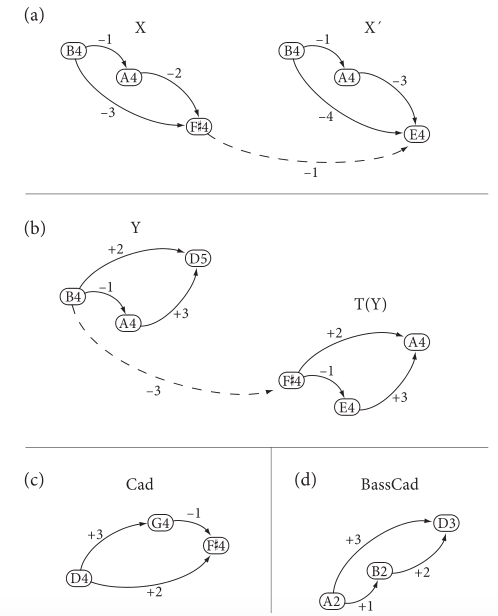
如果说这个分析范例更多表达了音高之间所发生的进程,那么下面的一个范例则将节奏上的比例作为更权重的观察。
Mozart,Symphony no.40,mvt.4,beginning of development(analysis:Lewin)
这是一个非常著名的片段,首先,可以看一下音高线条,向上减四,往下减七,一直重复,这充分体现了莫扎特喜爱的数字游戏,以及简短的不协和因素,其中暗含了连续的3音逆行倒影关联,这似乎与其后第二维也纳乐派韦伯恩的习惯性手段有着某种暗合,但这不是林斯教授关注的重点。在林斯教授出示的图例中,可以看到一些以节奏作为“interval”的一些布局。
DM指时值动机,RICH代表倒影逆行链,从图中可以看到DM的各种逆行与移位关系,其中倒影的逻辑不是唯一的,图中所列非常清晰,这里不赘述。以此脱离这个范例,以三位DM体现各种变型关联,如:
O R I RI
112 211 221 122
也可以更宏观的以短、长、长(SLL)为动机范例理解
O R I RI
SSL LSS LLS SLL
不难发现,以上的变形都是具有可逆性的,这也就指出,Involution是一种操作、转换,是可逆的。而可多次互逆的转换也就可以引出另外的一个话题——“新黎曼主义理论”Neo-Riemannian Theory,新黎曼理论,转换理论的分支,可以说是转换理论中最为人所知的一个理论,简称,NRT。新黎曼理论是将三和弦中的半音进行作了模型架构,主要关注三和弦,但在其发展进程中也希望能够扩展到其它更广泛区域,以三种转换:P,L,R为基础。(P,L,R转换手段以及新黎曼主义理论相关内容可见郭新教授“自然音七和弦声部进行的转换——用新黎曼主义理论的观点分析流行音乐中的和声进行”一文,2007年“黄钟”第4期)。
林斯教授以“新黎曼主义”从最初的产生、历史背景,中间的修改等方面,再到当前的理论运用与地位,进行了详尽的介绍。这样的一次详尽梳理,我以为是会为我们理清和声的很多其它方面提供了很大的帮助。
P,L,R的的转换较容易理解,也是“新黎曼理论”和声运用的基础。林斯教授同时对比的列出了我们熟悉的功能性连接与“新黎曼”式理解的连接想对应的图例。我们也许会很快的发现这两种方式中会有相同的结果,如图中圆圈所示,但这里不要忽略转换理论中强调的“箭头”方向,联系前文,可以提出一个“转换”的观点,也就是是否是“可逆”的,这应该是理解整个“转换理论”非常重要的一个角度。
理查德˙科恩继而提出了四个方位的循环圈,图中+/-代表大、小调,循环的方式是以P、L、R的模式进行,以这样的循环圈可以构成固定结构的六音列(Hexatonic),在循环圈内,对级的两个三和弦是没有重复音的,依旧是六音列的构成,这可以看作是“新黎曼理论”脱离功能连接理解的进一步延伸。
史蒂文˙林斯教授在下午的课程中用了大量的时间与实例来帮助我们理解“新黎曼理论”的具体运用。如,以下的和声进行:
如果用罗马字符标记,怎样理解这样的和声处理?我想答案是有的,但不会非常直接,可这样的和声也是舒伯特非常常见的运用。
林斯教授又以Lewin教授对于Wagner与Valhalla的实例展示了类似的用法。

在图中,我们看到运用P/L/R的转换,很容易得到以下的进行逻辑,有趣的是,这两个例子也得到了几乎一致的解释,图中底部横向与随后的向上纵向是LP的行进路径,可以看出这样的解释是非常直接有效的。之后再以瓦格纳Parsifal为例等等,这样的详细,均以不同的目标,比较式的运用不同的手段给予多样的理解。
史蒂文·林斯教授连续两天对于“转换理论” (Transformational)、“广义音程”(GIS)、“新黎曼理论”(NRT)等方面进行了清晰的讲解,能量密度极大,非常感谢林斯教授为此付出的精力,同时,也希望能够对于明天“音调感质和音调的泛化音程系统”(Tonal Qualia and a Tonal GIS)、“音调意图”(Tonal Intention)的课程内容有很好的理解。(文中所示图例大多以课程中教授课件的扫描形式修改而成,仅取文中涉及内容,非课件所示图片的完整形式)
(撰稿:王鹏 单位:天津音乐学院)



