
音乐理论人才培养项目课程综述(十五)
——未来的新想法
发布时间:2018-07-14 点击次数:103
2018年7月11日,上海音乐学院主办、上海音乐学院研究生部承办的“国家艺术基金音乐理论人才培养项目”进入了第十五天的项目培训课程。当天课程继续由前一天授课的德米特里?缇姆兹科教授(Dmitri Tymoczko)主讲,其现执教于普林斯顿大学,著有《音乐几何学》(A Geometry of Music)等论著。
当日课程中,缇姆兹科教授主要从以下几个方面进行了讲解和研讨,包括:声部进行的循环空间、声部进行在作品中的应用、新的音阶形式及其在肖斯塔科维奇作品中的运用。
一、声部进行的循环空间
首先,缇姆兹科教授指出声部进行有多种形式,包括bijective voice leading和non-bijective (数学名词“双射”与“非双射”)声部进行(见左下图)。

而就声部进行中的交错形式,缇姆兹科教授举例解释了他理解的声部交叉与传统理论中声部交叉模式的不同。传统认识中只有第二个是声部交叉形式,而以缇姆兹科教授的循环理念,在循环圈的模拟状态下,四个声部则都具有交叉进行。
接着,其就环形空间内的移动路径进行了讲解。继前两天课程讲述的第一种移动方式后(即沿着环形空间进行螺旋式移动),今天主要讲解了另外一种方式——对角线移动。对角线移动是指环形空间的横向移动,移动方式分为两步:第一步先把和弦看作是一个音阶,向下移动一次;第二步向上移动一个八度的N分之一(N代表和弦音的数量)。在这里缇姆兹科教授列举了三音和弦在十二音音阶中的移动,见下图:
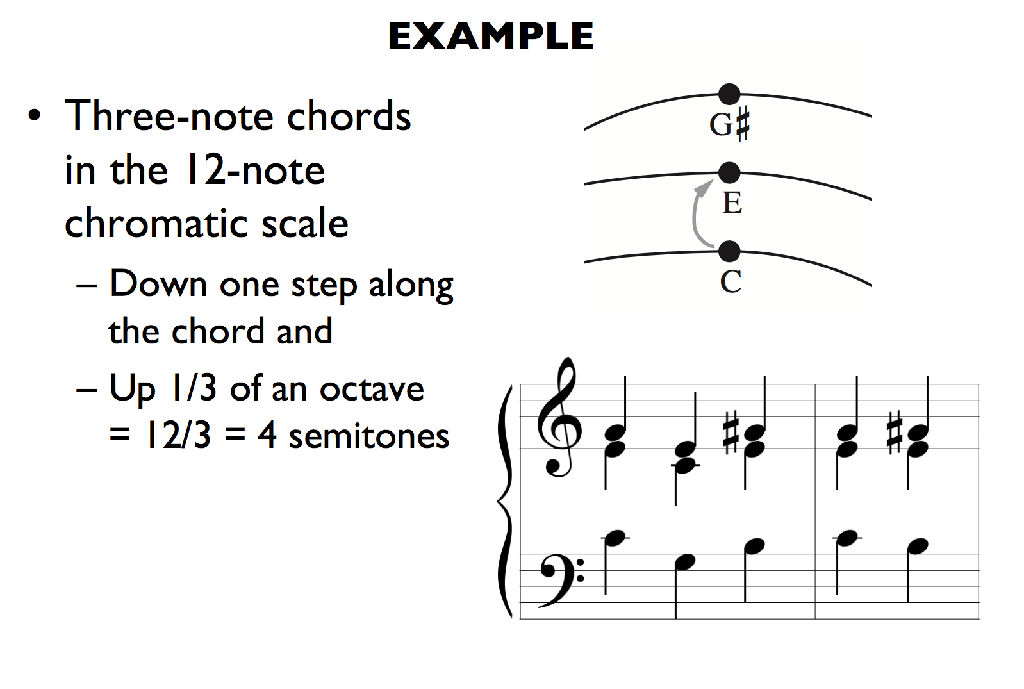
值得注意的是,如果音阶数与和弦音数不能够整除的情况下,移位后的和弦就不在开始的音阶中,因此需再次进行移位,对此缇姆兹科教授通过三音和弦在七音音阶中的移位进行了解读。
二、声部进行在作品中的应用
1. 环形空间的理论应用
环形空间为我们提供了在更广阔的条件下思考声部进行的统一工具,无论作曲家还是音乐理论家都可以运用环形空间理论进行创作以及分析,甚至可以应用于软件设计、游戏音乐的开发等相关领域。缇姆兹科教授指出,在看似类似的环形情况下我们可以进行相同的操作,同时这也为我们提供了一个探索不同和弦的空间,并在不同的音乐环境中构建类似的进程。
从创作的角度出发,假设随意在任何音阶上构成和弦,例如左下图中不协和七音和弦,这个和弦此时处于静止且被动的状态,我们不知道如何处理,这时环形空间就产生了作用。相同的和弦、相同的音级,音响效果却是非常不同的,有些协和而有些不协和。
通过上述认识,针对五声音阶与自然音阶,就能够知道如何运用相似的环形圈去创作。当这些环形看起来比较类似时,我们就能够清楚的了解和弦是如何进行移动的,五声音阶是五个五度的叠加,七声是七个五度的叠加,六声音阶的移动也是如此。
2.环形空间中的卡农现象
缇姆兹科教授指出,在环形空间中不断的、有规律的重复就会形成卡农(见左下图)。伴随着空间中的移动,我们会发现卡农现象,而且是非常常见的卡农。如果不停的以对角线的形式进行移动,就会形成右下图这种模式,这一模式是从新黎曼主义脱胎产生的结果。
下图为自然音阶四音和弦的卡农,每一个音阶都有着自己的卡农,缇姆兹科教授认为在古典音乐中,卡农扮演着十分重要的角色,旋律中的卡农很重要,因为它属于和声内部的进行。
3.图形设计及其对创作新思维的激发
在这一部分,缇姆兹科教授介绍了自己设计的图形是如何逐步完善表现出音阶以及和弦的。他表示下面的图形代表了七音音阶之间的声部进行关系,其中包含了自然音阶、泛音音阶、和声大调以及和声小调(见左下图)。但不久他发现,如果在自然音阶中将三音和弦通过图形画出来,则会出现同样的结果(见右下图)。后来缇姆兹科教授发现这个图不仅能够表示音阶,也是可以看出和弦的(是能够被八度整除的和弦)。大约在2015年,他意识到,无论音阶与和弦是否为整除关系,都可以使用相同的图形来表示音阶与和弦之间的关系,因此这个图也变得十分有意义。此后,缇姆兹科教授放弃了和弦是否能够被整除的要求,指出相同的声部进行模式可以在任何音阶的任何和弦中找到。由此,他表示对于数学家来说,几何学具有特别的意义,因为空间与距离是一种科学,这就为我们提供了另外一种思维方式,我们称之为拓扑学(没有距离的空间)。缇姆兹科教授强调他在做音乐几何学的时候就思考了相关方面的问题,考虑到极简的声部进行、移动以及特殊的和弦,认为这些可能对作曲家的创作更加有用。
接着他通过列举一个自然音阶三和弦的空间图来解读这种声部进行模式对作曲新思路的激发。左下图是自然音阶三和弦的空间图以及从上面俯视的平面图,数字表示和弦,从不同的角度看到不同的和弦。右下图是从上面看到的自然音阶三和弦,以及从正面看到的半音音阶三和弦。缇姆兹科教授指出,运用数字进行标注是因为我们看到的是非常复杂的图形,数字可以让我们清楚的看到相同与不同的和弦,这与音级集合的理论比较相似。利用这个模型可以将一个音阶移动到另外的音阶上,可以让我们超越在不同情境下所展示的可能性,运用更宽泛的眼光去分析与创作。
4.使用环形空间理论创作的作品
缇姆兹科教授在这里介绍了自己使用几何学及运用前文所阐述的理论创作的一部管弦乐作品(共五个乐章),以此探索其中的和声。他认为这种理论可以创作出具有层次感的音乐,这是属于21世纪的音乐。
下图是这部乐曲第一乐章开始部分所应用的和弦:
关于这部作品,缇姆兹科教授强调自己在创作中考虑最多的是这些理论的计算,他认为如果你的音乐体验是很神秘的,这是正常的,但对于音乐结构的感知则更加重要。自己创作这类音乐是希望听众通过聆听能够得到一些音乐感知,但这对于作曲家是具有挑战的,因为听众有可能对此难以理解。
三、新的音阶形式
除了自然音阶、五声音阶等大家熟悉的音阶之外,缇姆兹科教授还总结了十一音音阶和九音音阶的特点。九音音阶是把三和弦去掉之后得到的一个非常平均音阶,它共有三种模式,其中模式1和2是通过大小三和弦移出后得到的两个音阶,这三种九声音阶都包含有片段的八声音阶。
同时,缇姆兹科教授还讲解了八声音阶的三种扩大形式:
第一种,八声音阶本身;
第二种(模式1),由属音构成的两个八声音阶片段组成,包含C大调音阶与D旋律小调音阶(第七移位);
第三种(模式2),由主音构成的两个八声音阶片段组成,包含F大调以及F旋律小调音阶。
模式1与模式2是爵士乐中常用的被称为“改变的音阶”(altered scale),也是肖斯塔科维奇的作品中经常使用的。缇姆兹科教授以肖斯塔科维奇的《第七弦乐四重奏》为例解释了其在作品中的运用。他指出肖斯塔科维奇的做法经常是从一个八声音阶声部移动到另外一个八声音阶的声部,同时表示,想要有效的使用九音音阶,就要把八声音阶的片段拎出来进行分析。
另外,缇姆兹科教授在下午的课程中还以肖斯塔科维奇的作品为例,分析了21世纪音乐中的调性中心集合理论。这不仅仅是他未来的工作方向,同时也为我们青年理论学者提供了更加广泛的研究视角。
在最后的提问环节,缇姆兹科教授就学员们提出的如何定义宏观和声,怎样运用音乐几何学认识偶然音乐,关于即兴创作以及音乐几何学乃至类似建筑一类的“模型”是否能直接用于作曲等有关问题进行了详尽解答。虽然缇姆兹科教授的讲座已告一段落,但是短短三天精彩的讲座带领我们触摸了音乐几何学的神秘世界,为我们开启了音乐创作和研究的新思路。
(撰稿:杨静 单位:中国音乐学院)





